For general explanations see Summary.
Big-$\O$ vs. Big-$\Omega$ vs. Big-$\Theta$
Big-$\O$
- Upper bound
- Less than or equal: $\leq$
Big-$\Omega$ (Big-Omega)
- Lower bound
- Greater than or equal: $\geq$
Big-$\Theta$ (Big-Theta)
- Big-$\O$ AND Big-$\Omega$
- Tight bound
Notes
For an algorithm for which $\O(N)$ is valid, any greater term, e.g. $\O(N^2)$, is also valid (since Big-$\O$ is an upper bound, that is, less than or equal).
For an algorithm for which $\Omega(N)$ is valid, any smaller term, e.g. $\Omega(1)$, is also valid (since Big-$\Omega$ is a lower bound, that is, greater than or equal).
However, in practice, the tightest possible bounds are usually used. That is, the smallest term for Big-$\O$ and the largest term for Big-$\Omega$.
Rules for determining the Big-$\O$/$\Omega$/$\Theta$ term
1. Drop Constants
- $\O(2N)$ becomes $\O(N)$
- Because, no matter how much the constants of e.g. $2\,000\,000 N$ and $2N^2$ differ, with growing input size $N$, the latter term will eventually surpass the former one.
- We are interested in the order of growth only of the running time, and with large $N$, constants and non-dominant terms become relatively insignificant.
2. Drop Non-Dominant Terms
- $\O(N^2 + N)$ becomes $\O(N^2)$
- $\O(5\cdot2^N + 3N^{100})$ becomes $\O(2^N)$
- $\O(A^2 + B)$ stays $\O(A^2 + B)$
- Explanation, see above
3. Different Steps of an Algorithm are Added
- Two successive for loops taking A and B iterations, respectively: $\O(A + B)$
4. Nested Steps in an Algorithm are Multiplied
- Two nested for loops taking A and B iterations, respectively: $\O(A \cdot B)$
5. Use Different Variables for Different Inputs
- For example, if the input consists of two strings of length $n$ and $m$, use two variables $N$ and $M$
- For example, $\O(N + M)$
Addtional Rules
Base of Logarithm
The base of a logarithm doesn’t matter: log denotes a logarithm of any base.
Base of Exponent
The base of an exponent matters: $\O(2^N)$ and $\O(8^N)$ are different.
Non-Dominant Terms in Exponent
Non-dominant terms in an exponent don’t matter: $2^{N+1}$ becomes $\O(2^N)$.
Constants in Exponent
Constant factors in exponents matter: $\O(8^N)$ and $\O(8^{2N})$ are different.
Common Big-$\O$/$\Omega$/$\Theta$ Terms and Their Relation
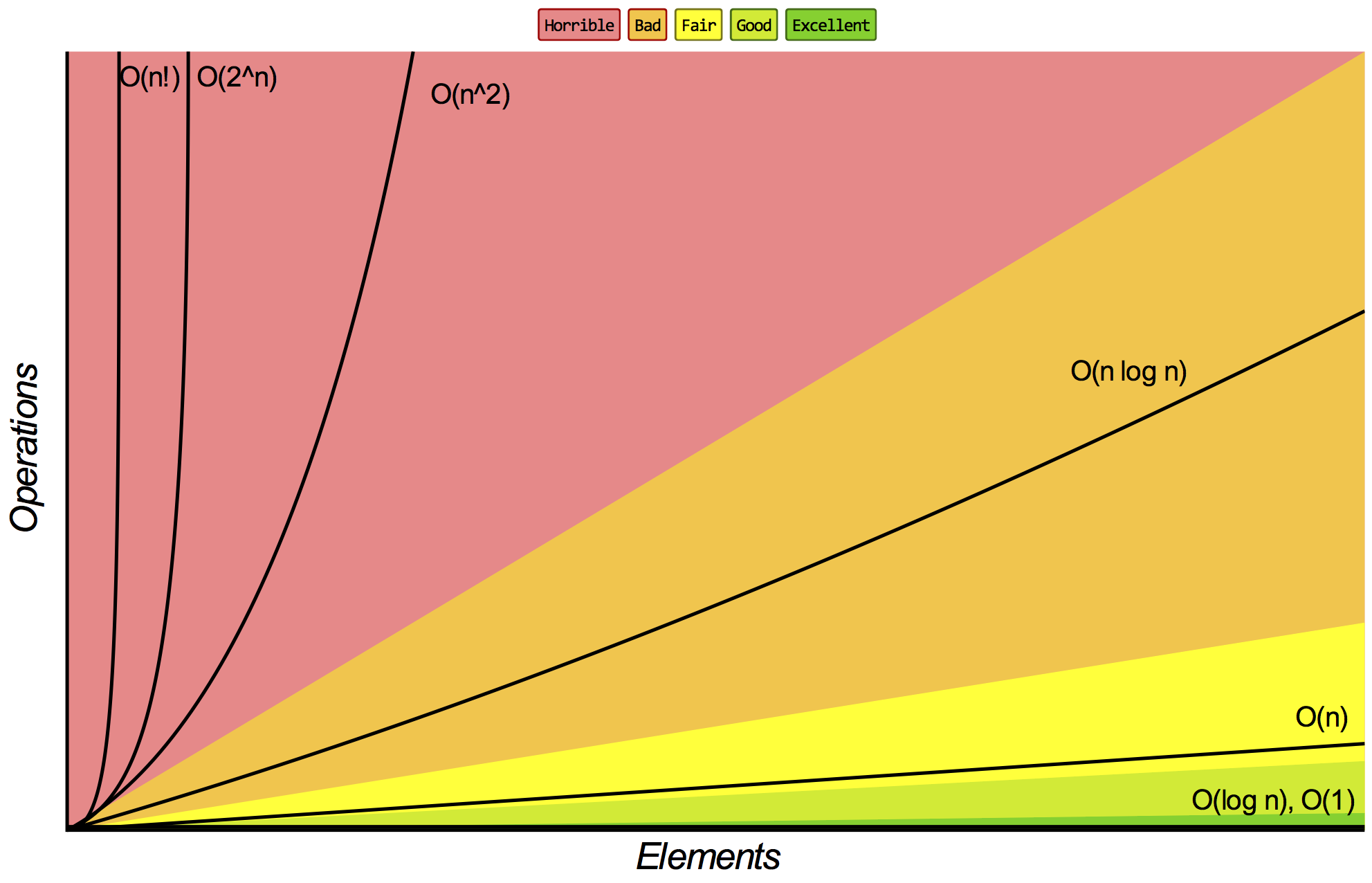Source: bigocheatsheet.com
Summary
What is it all about?
Big-$\O$/$\Omega$/$\Theta$ notation is used to express complexity bounds of an algorithm.
The term within the Big-$\O$/$\Omega$/$\Theta$ notation denotes a number of steps (time complexity) or used memory units (space complexity).
The variables within the term are are the sizes of the inputs of the algorithm.
What’s the difference between $\O$, $\Omega$, and $\Theta$?
$\O$, $\Omega$, and $\Theta$ defines what the term inside the notation means (see here):
- $\O$: the real value is less than or equal to the notation term (the term is an upper bound)
- $\Omega$ the real value is greather than or equal to the notation term (the term is a lower bound)
- $\Theta$ the real value is equal to the notation term (the term is a tight bound)
How to understand the term within Big-$\O$/$\Omega$/$\Theta$?
However, the Big-$\O$/$\Omega$/$\Theta$ term is not an exact term. Its purpose is to indicate an order rather than an exact value.
That’s why we apply the rules listed here to the Big-$\O$/$\Omega$/$\Theta$ term.
For example, if the tightest upper bound for an algorithms would really be $2N^2$, the Big-$\O$ term is just $\O(N^2)$. Now, if the maximum number of steps of this algorithm is exactly $2N^2$, the algorithm is still in $\O(N^2)$ (even though $2N^2 \leq N^2$ is false).
Conclusion: don’t take the Big-$\O$/$\Omega$/$\Theta$ literally, but just as an indication of order or category.
References
- Great video: YouTube - Big O Notation