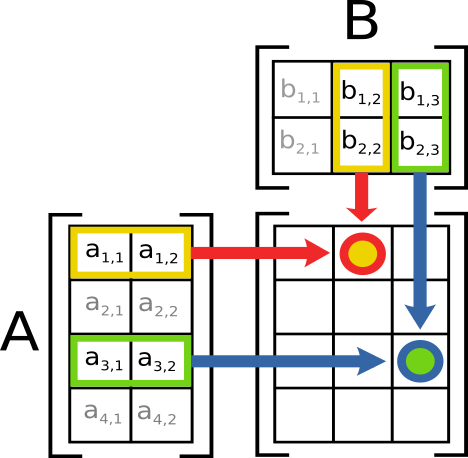
How To Multiply Two Matrices?
$m\times n$ matrix:
- $m$: number of rows (nrow)
- $n$: number of columns (ncol)
Multiplication of two matrices $m_1 \times n_1$ and $m_2 \times n_2$ is possible if either:
- $m_1 = n_2$ (i.e. nrow of 1st matrix = ncol of 2nd matrix)
- $n_1 = m_2$ (i.e. ncol of 1st matrix = nrow of 2nd matrix)
The resulting matrix always has:
- $m_1$ rows
- $n_2$ columns
1x4 and 4x2 Matrix
1x4
4x2 $\rightarrow$ OK
1 5 4x2 matrix
4 3
3 1
3 2
+------
1x4 matrix 4 2 5 2 |33 35 ==> Result: 1x2 matrix
4x1 and 4x2 Matrix
4x1
4x2 $\rightarrow$ Nope
1 5 4x2 matrix
4 3
3 1
3 2
+------
4x1 matrix 4 |
2 |
5 |
2 | ==> Does not work!
1x4 and 2x4 Matrix
1x4
2x4 $\rightarrow$ Nope
1 4 3 3 2x4 matrix
5 3 1 2
+------------
1x4 matrix 4 2 5 2 | ==> Does not work!
4x1 and 2x4 Matrix
4x1
2x4 $\rightarrow$ OK
1 4 3 3 2x4 matrix
5 3 1 2
+------------
4x1 matrix 4 |24 28 16 20
2 |12 14 8 10
5 |30 35 20 25
2 |12 14 8 10 ==> Result: 4x4 matrix
\hfil \textit{Swap first and second matrix of above multiplications.} \hfil
4x2 and 1x4 Matrix
4x2
1x4 $\rightarrow$ OK
4 2 5 2 1x4 matrix
+------------
4x2 matrix 1 5 |24 12 30 12
4 3 |28 14 35 14
3 1 |16 8 20 8
3 2 |20 10 25 10 ==> Result 4x4 matrix
4x2 and 4x1 Matrix
4x2
4x1 $\rightarrow$ Nope
4 4x1 matrix
2
5
2
+---
4x2 matrix 1 5 |
4 3 |
3 1 |
3 2 | ==> Does not work!
2x4 and 1x4 Matrix
2x4
1x4 $\rightarrow$ Nope
4 2 5 2 1x4 matrix
+------------
2x4 matrix 1 4 3 3 |
5 3 1 2 | ==> Does not work!
2x4 and 4x1 Matrix
2x4
4x1 $\rightarrow$ OK
4 4x1 matrix
2
5
2
+---
2x4 matrix 1 4 3 3 |33
5 3 1 2 |35 ==> Result: 2x1 matrix