Overview of the most important data structures.
Contents
- Contents
- Binary Heap
- Binary Search Tree
- Stack vs. Queue vs. Priority Queue
- Priority Queue
- Stack
- Queue
Binary Heap
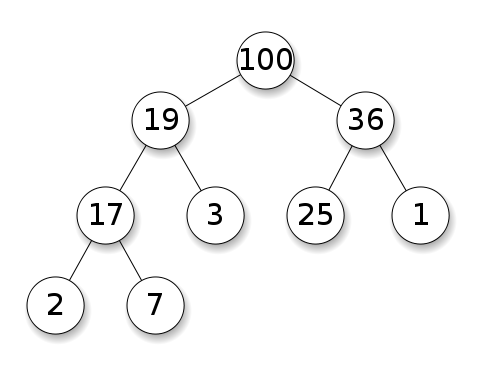
Max-Heap
- The key of every node is larger than or equal to the keys of its children
- Consequently, the key of every node is less than or equal to the key of its parent
- Moving up from any node yields a non-decreasing sequence of keys
- Moving down from any node yields a non-increasing sequence of keys
- The node with the largest key is at the root
Min-Heap
Idem max-heap, but with comparison relation inversed.
Representation
A binary heap can be represented as an array to get rid of the need for pointers (which use precious space).
The “pointers” are implicit in the array indices, as follows:

- Index 0 of array is left empty
- Root (depth 0) is at index 1
- Nodes on depth 1 are at indices 2, 3
- Nodes on depth 2 are at indices 4, 5, 6, 7
- Nodes on depth 3 are at indices 8, 9, 10, 11, 12, 13, 14, 15
- etc.
Thus, a binary heap of size $n$ can be represented as an array of size $n+1$ (the convention of leaving array index 0 empty is optional, but simplifies the pseudo-pointer arithmetic below).
Pseudo-Pointer Arithmetic
Get depth of node given an index:
\[\newcommand{\Log}{\text{log}} \newcommand{\mr}[1]{\mathrm{#1}} \mr{depth} = \left\lfloor\Log_2(\mr{index})\right\rfloor\]Get index of parent node (if any) given an index:
\[\mr{parent} = \left\lfloor\frac{\mr{index}}{2}\right\rfloor\]Get indices of left and right children (if any) given an index:
\[\mr{leftChild} = 2 \times \mr{index}\] \[\mr{rightChild} = (2 \times \mr{index}) + 1\]Note
It’s possible to represent any binary tree in an array as shown above, so why we don’t represent binary search trees (BST) as arrays?
Because for heaps, each level can be fully packed, and the length of the array to represent a binary tree with $k$ levels is around $2^k$. A heap of size $n$ has $\left\lceil\Log\, n\right\rceil$ levels, and thus requires an array of length $2^{\left\lceil\Log\, n\right\rceil}$.
However, for an unbalanced BST, the levels cannot be fully packed, because there is no flexibility for the position of the nodes. In the worst case, a BST of size $n$ has $n$ levels, and thus requires an array of length $2^n$.
Applications
- Used to implement the priority queue data type
- Used for the heapsort sorting algorithm
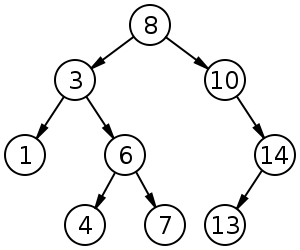
Binary Search Tree
Stack vs. Queue vs. Priority Queue
All of them have an insert operation, which adds a new value to the data type:
- Stack: push
- Queue: enqueue
- Priority queue: enqueue
All of them have a remove operation, which removes a value from the data type:
- Stack: remove newest (called pop)
- Queue: removed oldest (called dequeue)
- Priority queue: remove maximum (called dequeue)
Priority Queue
Insert items, remove the item with the highest/lowest key.
Applications
- Discrete event simulator: the key is the event time
- Job scheduler: the key is the priority of a job waiting for execution
- Sorting problem: insert elements to be sorted in a priority queue with the key being the value for which to sort, then repeatedly remove the minimum element from the priority queue
Can be implemented with the binary heap data structure.
Time Complexity
Depends on the implementation:
- Unsorted array implementation
- Insert: $O(1)$
- Remove min/max: $O(n)$
- Sorted array implementation
- Insert: $O(n)$
- Remove min/max: $O(1)$
- Binary heap implementation
- Insert: $O(\Log \, n)$
- Remove min/max: $O(\Log \, n)$
Stack
Insert items, remove the newest item (most recently inserted).
Time Complexity
- Insert (push): $O(1)$
- Remove (pop): $O(1)$
Applications
- Reverse a list: push all items on a stack, and then pop them
Queue
Insert items, remove the oldest item (least recently inserted).
Time Complexity
- Insert (enqueue): $O(1)$
- Remove (dequeue): $O(1)$